三角函数最有用的一集•测距简史

无论是冷兵器时代的弓箭，还是现代的狙击枪、火炮，如何得到两点间的距离永远是打准的必要条件。

🐢：谁会不想用这玩意开上一炮呢？

而测距的方式，也随着科技的进步和精度需求的增长，变得多种多样。

跳眼法

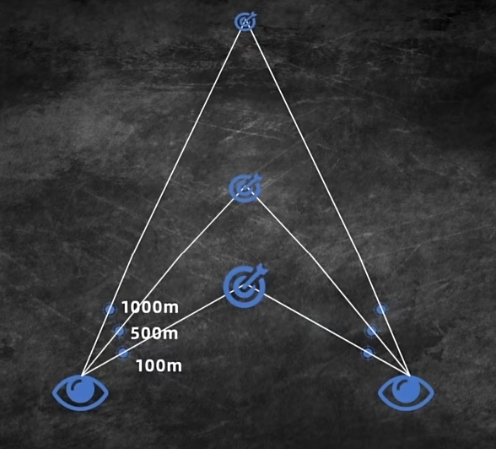
众所周知，如果某人给你竖拇指，他不一定在夸你，可能在瞄准你。伸直胳膊，竖起大拇指，跳眼测距并不复杂。会了相似三角形，你就一定也能理解它的原理。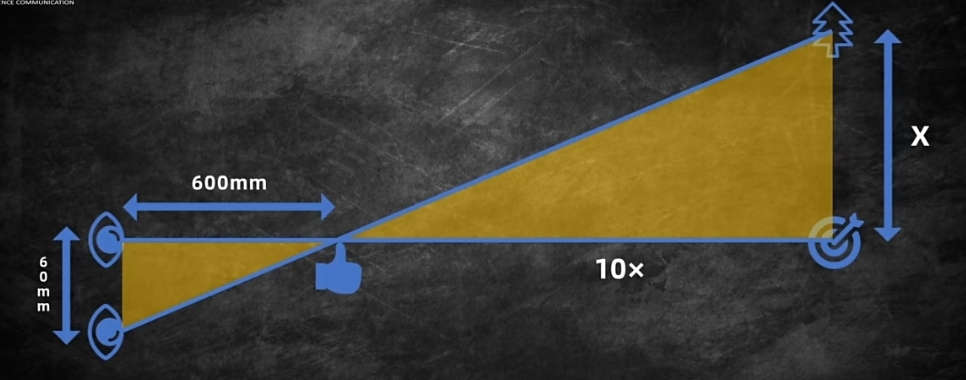

跳眼法的基础来自于两眼的视差。人的瞳距大概是60mm，而臂长大约是600mm，因此，只要了解生活中常见物体的长度，你就可以测出距离来上一炮。（🐢：我缺的是怎么测距吗，是炮！）

密位测距的原理与跳眼法差不多，不过，除了相似三角形，我们还要用到一点弧度制。在这里，我们定义一个角度单位，毫弧度（密位），1毫弧度所对应的弧长，等于这个圆半径的千分之一。那么这个角度大约是多大呢？化成角度制就是\frac{360}{6175}度。

在瞄准镜中，有许多分划线。

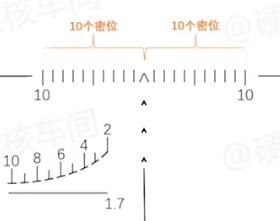
假设两个分划线之间为1密位，那么，如果一名肩宽50cm的成年哺乳动物对应1密位，他离我们有多远呢？

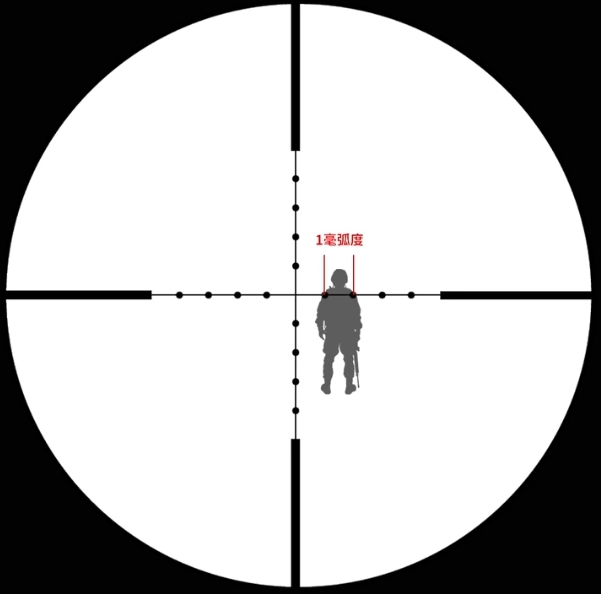
答：50cm×1000＝500m

🐢：很简单吧

当然，将圆分为6175份还是复杂了些，因此，现在常用的北约提出的密位大约是圆周的六千分之一。

讲完了密位测距，现在是偷懒教学时间——斜坡测距。

像本段第一幅图左下角的那段弧线就是用来进行斜坡测距的标尺，它的原理简单来说就是近大远小。

1,7指假设人的身高为170cm，将视野内的人正好夹在标尺之间，上面的数字x100便是距离了。

光学测距仪

提到光学测距仪，最著名的就是大和号上来自Nikon的“93式15米基线倒分像立体测距仪”。

🐢：就是左右两侧伸出来的那个

让我们来一个一个词解析一下。

“93式”emm。。。让我们略过它。

“15米基线”，这就是光学测距仪精准的基础。光学测距仪大致可分为两类，立体测距仪和合像测距仪。让我们先从合像测距仪说起。

合像测距仪只有一个目镜，两个物镜就相当于两个望远镜，对于不同的合像测距仪两个像也有所区别，可能是上半部分和下半部分，也可能是两个完整的像。

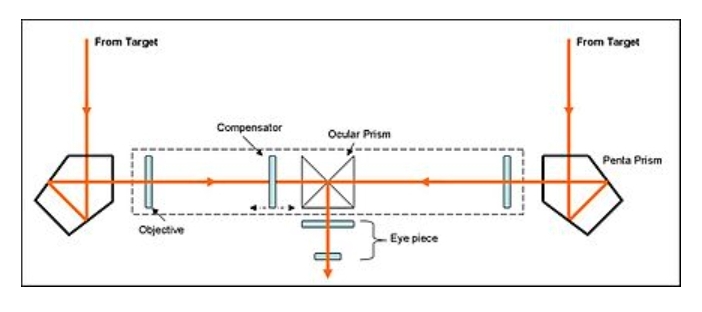
在这张图中右镜筒可以旋转并从刻度盘中读出旋转角度θ。

当我们旋转其中一个镜筒直至两个像重合时，便可以根据θ的大小算出距离L。

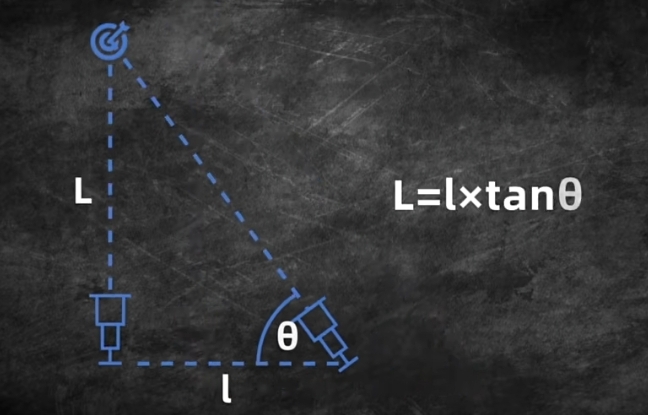
这里的l就是基线长度。

下面，让我们来开始一次测量。（🐢：上图！）

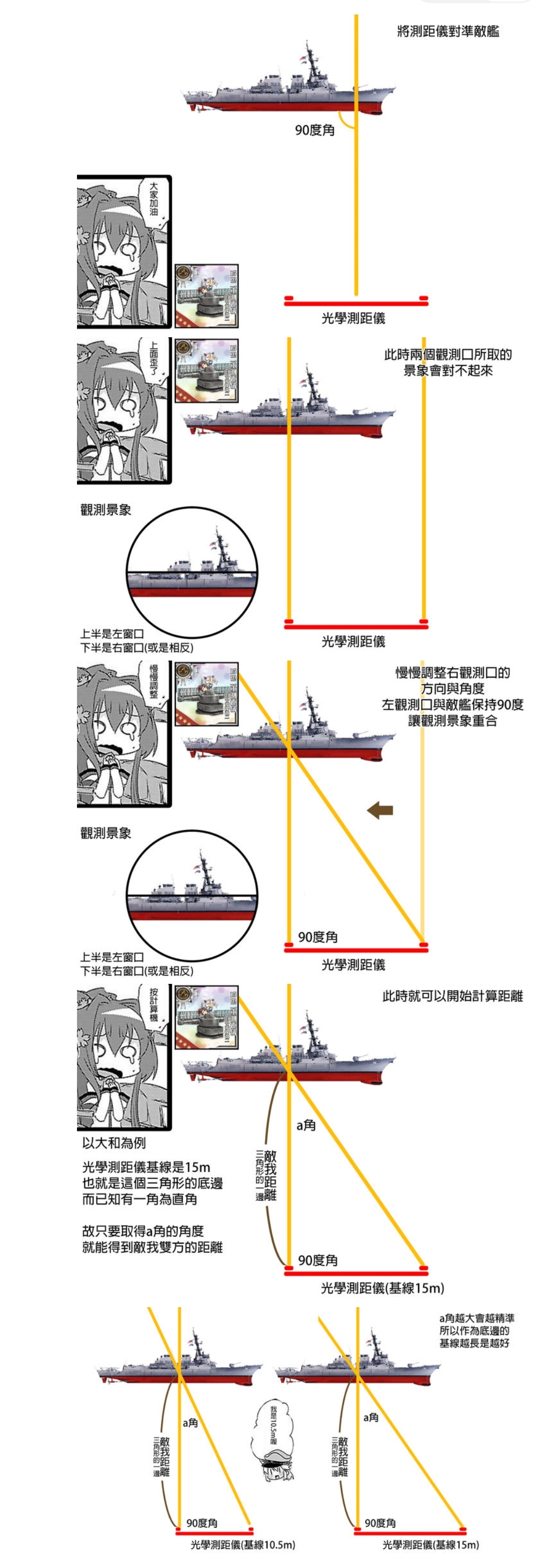
在了解完合像测距仪后，让我们继续。

显然，这种测距方式有一个缺点，就是需要旋转镜筒，因此，立体测距仪以其快速反应的优势现在也被部队所采用。

其实大和号使用的应当算是二重测距仪，即“倒分像”一词描述的是合像测距仪种类，而同时，这又是一台立体测距仪。

立体测距仪有两个目镜，同时有若干标尺。在这里，让我们先做个实验。

伸出你的一根手指，举在两眼之间，不用特别近，保证你能清晰的看到它。（🐢：斗鸡眼加载中）

现在，离你较远的墙面应当是模糊的。保持手指不动，尝试去看清远处的墙面。

咦？手指变成了两根？这就是立体测距仪的基础，立体视觉。

在立体测距仪中，若是我们选择看清1km外的事物，代表近距离的标尺就会变成两个。

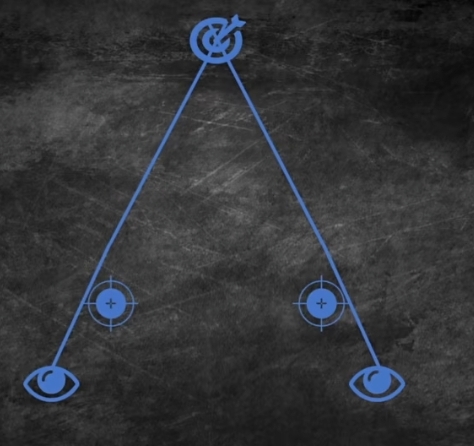
而若是选择看清标尺，远处的事物也会变成两个。

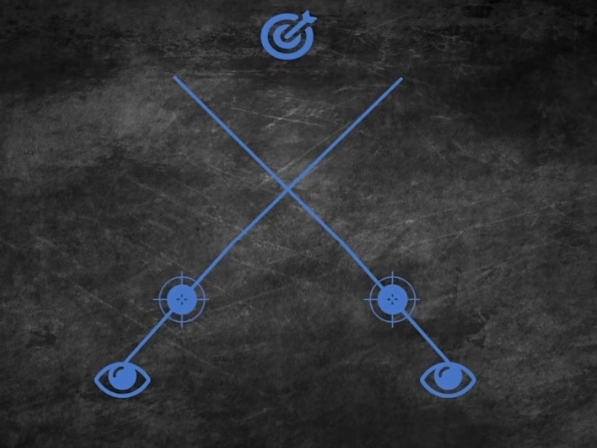
因此，只要刻上一系列的标尺，就可以实现测距。

很简单吧！到这里，光学测距仪就大致讲完了，不过，无论是那种测距仪，都需要严格训练才能熟练使用，因此，我们需要一些能直接读出距离的东东。

嘿嘿嘿，Laser来喽

TOF激光测距仪，原理极其简单，从名字就能看出来，Time Of Fly，光速乘时间除以二，使用更不用说，按个钮的事，可你有没有想过，这么短的时间是怎么被记录的？

粗暴一点，我们可以用上精度更高的时钟。这种方法被称为dTOF（直接飞行时间）。

如果用手电筒一直去照射一面墙，谁也分不清哪个光子是什么时候发射的。因此，我们可以把手电筒开关开关不断重复，这就是脉冲。

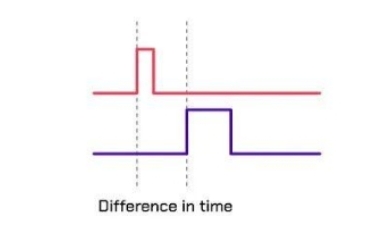
从发射脉冲开始计时，收到时停止，便可以计算出距离了。

dToF的原理看起来虽然很简单，但是实际能达到较高的精度很困难。除了对计时有非常高的精度要求以外，还对脉冲信号的精度有很高的要求。普通的光电二极管难以满足这样的需求。所以，这玩意不可能便宜。因此，在手机等设备上，更常用的是iTOF（间接飞行时间）。

假如我们可以以正弦波调制发射出去的激光，那么，只需要测量发射的正弦波与接收的正弦波之间的相位差就可以推出激光的飞行时间。

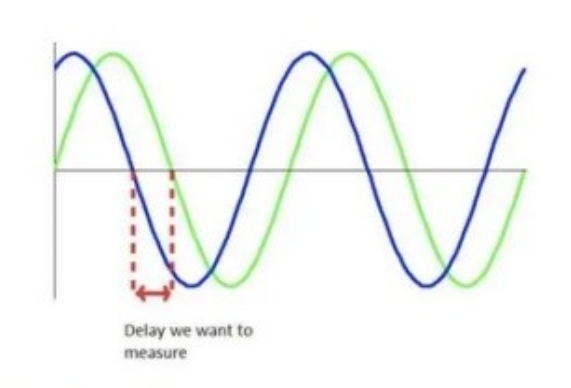
而要做到测量相位差，其实并不困难。下面是一种比较巧妙的方式：

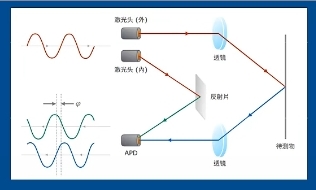
在测出相位差后，距离的计算只需要一个小小的公式d = L_{\text{s}} \left( N + \frac{\Delta \phi}{2\pi} \right) （🐢：还挺简洁？）

在这个式子里， L_{\text{s}}表示测尺长，即二分之一波长，N表示测尺个数。

但这里有个问题，N无法被测量。因此，我们要让N取最小，即测量距离小于测尺长。可是，因为相位差的测量精度有限，所以，相位测距的精度大致等于\frac{L_{s}}{1000} ，即测尺无法在保证精度的前提下无限延长。

那么，还有什么办法吗（🐢：你来帮帮我？）

锵锵，三角测距你值得拥有。

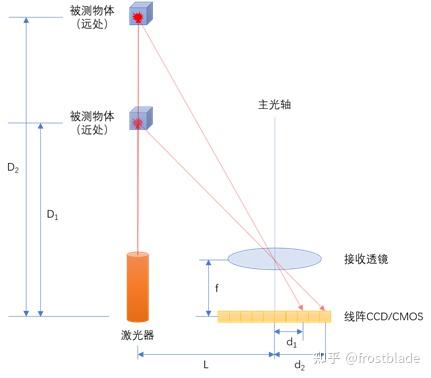
这就是直射式三角测距，原理如图所示。还是一点简单的相似三角形知识就可以理解。但在实际情况下，为了充分利用线阵传感器的性能，一般选择倾斜放置传感器。

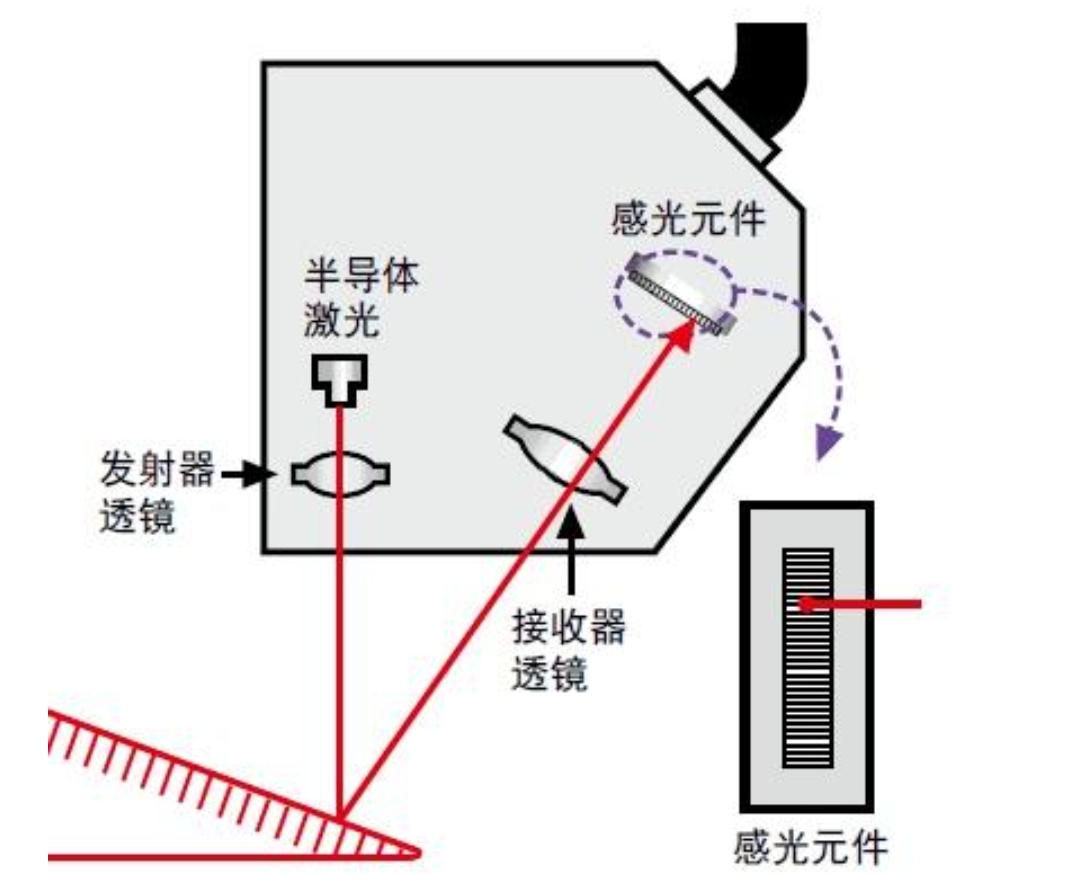
在此基础上还衍生出了斜射式三角测距。

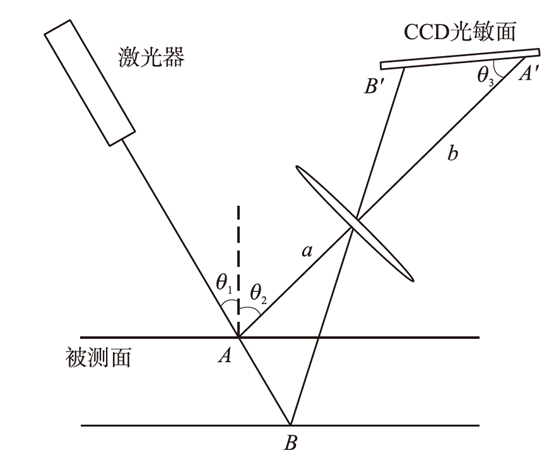
同样一点简单的三角函数运算就能解决。

其他的现代测距方式如超声测距仪的原理本质上也是TOF罢了，便不再重复。（🐢：偷个懒，哈哈）

总结一下

测距工具，历代乃兵家研发之重点。优劣好坏，难以论说。但科学家无不注意到，正是在这极小的误差上，决定了多少次战斗的胜负兴亡。在现代科技的加持下，真可谓占尽天时。这种勃勃生机，万物竞发的境界，就在眼前。无论怎么讲，测距工具是一代强上一代，优势在我。